Свертка с функцией разрешения

В этом задании Вам предстоит изучить влияние ошибки измерения на наблюдаемую форму сигнала. В эксперименте происходит измерение плотности распределения f(x) некоторой случайной величины. Для этого выполняют множество измерений этой величины. Измерительный прибор не идеален, он вносит случайную ошибку в измерение с плотноснотью вероятности g(xi). Это приводит к тому, что наблюдаемая форма распределения отличается от истинной f. Наблюдаемая форма может быть найдена с помощью свертки функций f и g.

В качестве сигнального распределения f(x) будем рассматривать два варианта:

Для разрешения прибора g(xi) также будем рассматривать два варианта:

И сигнальные распределения и функции разрешения описываются двумя параметрами: средним значением и параметром, характеризующим ширину распрелеоения.

Базовая версия

Решите эту задачу рамках объектно-ориенториванного подхода. Базовая версия решения требует реализации классов Generator и Plotter. Первый отвечает за вычисления, а второй - за визуализацию.

Минимальная сигнатура класса Generator:

class Generator:
    def __init__(self, mean, width, bias, variance, sigtype, restype, nsigma):
        """ Аргументы:
          - mean:float и width:float - отвечают за среднее значение и ширину
            сигнального распределения, соответственно
          - bias:float и variance:float - отвечают за среднее значение и ширину
            функции разрешения, соответственно
          - sigtype:int - определяет сигнальное распределение:
            - значение 0 соответствует нормальному распределению
            - значение 1 соответствует распределению Коши
          - restype:int - определяет сигнальное распределение:
            - значение 0 соответствует нормальному распределению
            - значение 1 соответствует распределению Мояля
          - nsigma:float - определяет ширину окна для вычисления функций:
            [mean - nsigma*width, mean + nsigma*width] и
            [-nsigma*variance, nsigma*variance]
        """
        pass

Экземпляр класса Generator должен иметь следующие атрибуты:

x:np.ndarray - значения, для которых вычислены сигнальные распределения (до и после свертки с функцией разрешения)
signal:np.ndarray - значения сигнального распределения в точках x
smeared_signal:np.ndarray - значения измеренного распределения в точках x, полученные с помощью свертки функций f и g
xi:np.ndarray - значения, для которых вычислена функция разрешения
reso_pdf:np.ndarray - значения функции разрешения в точках xi

Минимальная сигнатура класса Plotter:

class Plotter:
    def __init__(self, gen, fig, ax):
      """ Аргументы:
        - gen:Generator
        - fig:Figure
        - ax - массив из двух объектов Axis, связанных с объектом fig
      """

    def plot(self):
      """ Выполняет отрисовку """

Отрисовка должна выполняться на двух объектах Axis, расположенных в одном окне. На одних осях расположены сигнальные распределения до и после свертки с функцией разрешения, а на других должна быть показана функция разрешения. Итоговый вариант может выглядеть, например, так:

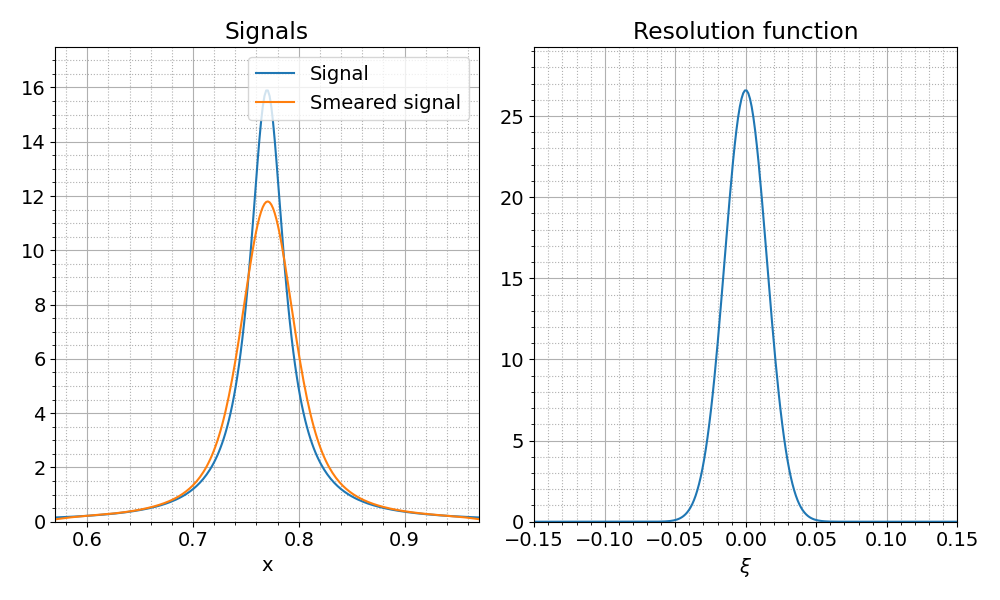
example

Указания 1

Решение должно находиться в файле convolution.py
Для вычисления плотности вероятности различных распределений используйте функции stats.norm.pdf, stats.cauchy.pdf и stats.moyal.pdf из модуля scipy.stats
Для выполнения дискретной свертки используйте функцию scipy.signal.convolve или scipy.signal.fftconvolve с аргументом mode='same'
Для достаточно больших значений параметра nsigma (скажем, больше 5) нормировка сигнального распределения не должна существенно изменяться после свертки с функцией разрешения. Чтобы соблюсти верную нормировку результат функции convolve необходимо умножить на размер шага по x.
Подумайте в каких точках необходимо вычислять функцию разрешения g(xi) для свертки с сигнальным распределением f(x). Шаг по переменным x и xi должен быть одинаковым

Как тестировать решение локально

Работа класса Generator может быть протестирована стандартным способом. Устанавливаем необходимые пакеты:

pip install -r requirements.txt

Запускаем тесты:

pytest -vs

Реализация класса Plotter проверяется преподавателем.

Дополнительное задание

Вы создали инструмент для изучения влияния ошибки измерения на наблюдаемый сигнал. Давайте получим еще больше информации об этой процедуре. Добавьте в класс Generator вычисление для сигнального распределения (до и после свертки с функцией разрешения):

Положения максимума
Положения среднего значения
Полной ширины на полувысоте (FWHM - full width at half maximum)

Результаты вычислений выводите в консоль.

Указания 2

Рассмотрите следующий способ вычисления FWHM:
- Используйте класс CubicSpline из модуля scipy.interpolate для создания сплайна сигнального распределения, из которого вычтена половина от максимального значения. Так, чтобы точки, соответствующие полувысоте, имели нулевые значения по вертикальной оси
- Используйте метод roots объекта CubicSpline для вычисления нулей функции сплайна. Расстояние между двумя полученными значениями и будет равно FWHM
- Из-за особенностей алгоритма построения сплайна на границах диапазона могут появиться дополнительные нули. Эту ситуацию необходимо отследить и обработать при необходимости

Продвинутая версия

В продвинутой версии необходимо реализовать графический интерфейс пользователя (GUI), с помощью которого можно будет изменять параметры системы. Для этого надо будет добавить функциональность в класс Plotter и создать класс SmGui, который будет отвечать за графический интерфейс.

Реализовать GUI можно различными средствами. Например:

Виджеты matplotlib. Этот вариант наиболее простой в реализации, но даже небольшое количество виджетов приводит к сильному замедлению работы программы
Библиотека tkinter. Для этого варианта объект matplotlib.Figure необходимо будет встроить в окно Tk
Библиотека PyQt5. Эту библиотеку необходимо установить отдельно. В этом варианте также необходимо будет встроить объект matplotlib.Figure в окно Qt5. Больше примеров можно найти здесь.

Покажем несколько примеров GUI. Виджеты matplotlib:

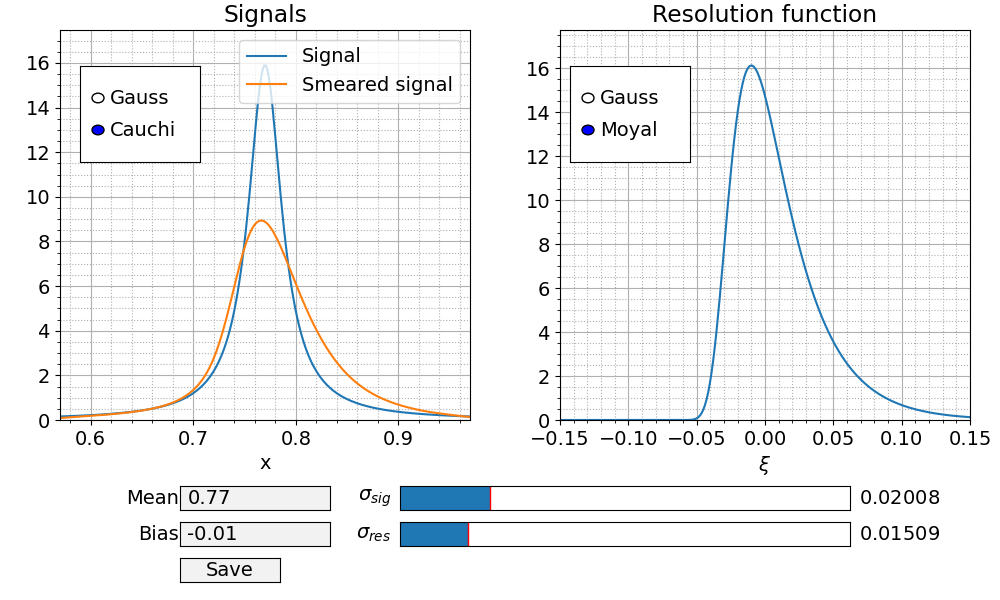
example

С библиотекой tkinter:

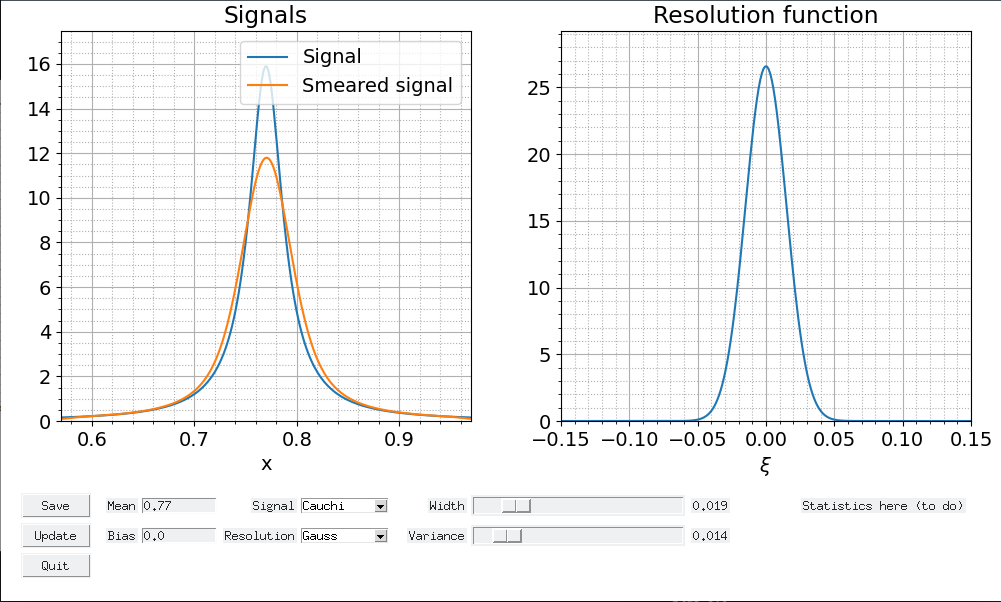
example

С библиотекой PyQt5:

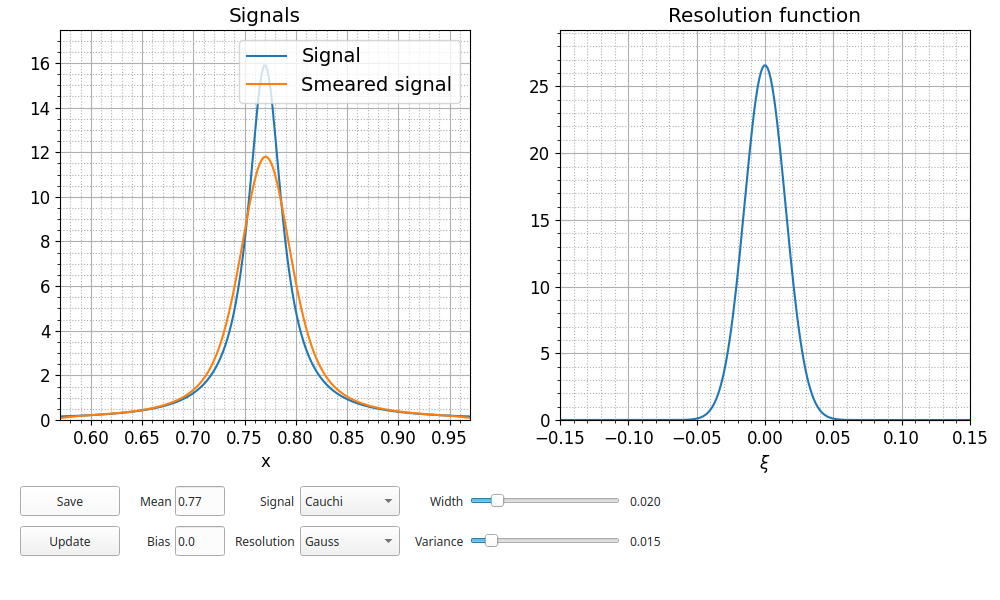
example

Нет необходимости копировать эти примеры. Вы можете самостоятельно разработать интерфейс.

При интерактивной работе необходимо много раз обновлять графики и изменять диапазоны значений осей. С диапазонами значений проблем не должно возникнуть. А вот обновление графиков требует внимания. Просто создавать новые графики не получится, поскольку они будут отображаться поверх предыдущих. Объекты Line2D (которые создаются функцией pyplot.plot) имеют методы set_xdata и set_ydata, позволяющие задать новые данные. После обновления всех графиков нужно выполнить отрисовку, например, так:

figure.canvas.draw_idle()

Класс Plotter должен иметь метод update, который обновляет все графики.

Указания для работы с виджетами matplotlib

В этой задаче могут оказаться полезными виджеты TextBox, Button, Slider. Конструктор любого виджета matplotlib первым параметром принимает объект Axes, который определяет размер и положение виджета.

Чтобы связать виджет с логикой программы необходимо связать с ним функции, которые должны вызываться при определенных событиях. Например:

Методы on_text_change и on_submit виджета Виджет TextBox принимают callable объект для вызова при изменеии текста и при нажатии клавиши Enter, соответственно
Метод on_clicked виджета Button
Метод on_changed виджета Slider

Ссылка на объект виджета должна быть доступна в течение времени исполнения программы, чтобы виджет был активен.

Подробное описание и примеры смотрите в документации.

Указания для работы с tkinter

Минимальный пример встраивания графика matplotlib в программу с tkinter находится в файле tkinter_example.py. Рассмотрите использование виджетов tkinter.Label, tkinter.Entry, tkinter.Button и tkinter.Scale. Виджеты tkinter.Scale и tkinter.Button можно связать с callback-функциями через параметр конструктора command:

s = tkinter.Scale(master=master, command=callable)
b = tkinter.Button(master=master, text=text, command=callable)

Задать и прочитать содержимое виджета tkinter.Entry можно с помощью методов insert и get, соответственно.

Метод bind позволяет связать виджет, событие и действие (callback-функцию). Так, например, можно связать главное окно программы, некоторое действие и нажатие клавиши Enter:

class Gui(tkinter.Tk):
    def __init__(self):
        super().__init__()
        self.bind('<Return>', callable)

Указания для работы с PyQt5

Минимальный пример встраивания графика matplotlib в программу с PyQt5 находится в файле pyqt_example.py. Рассмотрите использование виджетов QPushButton, QSlider, QLabel, QLineEdit из модуля PyQt5.QtWidgets.

Связать эти виджеты с callback-функциями можно следующим образом:

button = QPushButton(label, parent)
button.clicked.connect(callable)

qle = QLineEdit(init, parent)
qle.textChanged.connect(callable)
qle.returnPressed.connect(callable)

sld = QSlider(Qt.Vertical, parent)
sld.valueChanged.connect(callable)

Класс FFPlotter удобно сделать наследником класса FigureCanvasQTAgg из модуля matplotlib.backends.backend_qt5agg, как показано в примере. Класс SmGui удобно сделать наследником класса QMainWindow из модуля PyQt5.QtWidgets.

В примере GUI выше реализовано сохранения окна в графический файл. С библиотекой PyQt5 снимок окна программы можно выполнить с помощью объекта QPixmap из модуля PyQt5.QtGui. Вот так может выглядеть метод класса SmGui для сохранения снимка окна:

class SmGui(QMainWindow):
    # ...
    def save(self):
        pix = QPixmap(self.size())
        self.render(pix)
        pix.save('ffilter.png', 'png')

Свертка с разрешением (5)

Свертка с функцией разрешения

Базовая версия

Указания 1

Как тестировать решение локально

Дополнительное задание

Указания 2

Продвинутая версия

Указания для работы с виджетами matplotlib

Указания для работы с tkinter

Указания для работы с PyQt5